1 引言
從20世紀(jì)下半葉起,各種類型的高速船紛紛面世并投入使用,其航速和尺寸均呈增長的趨勢[1]。高速船具有很多優(yōu)勢,如高航速,甲板面積寬敞,優(yōu)越的耐波性、快速性和操縱性,需求量正逐年增加,但是,在不斷的使用過程中,發(fā)現(xiàn)了其不盡人意之處,噸位較小的船在大風(fēng)浪中存在劇烈的搖蕩運(yùn)動,如縱搖和高速下的垂蕩問題,這些運(yùn)動會使船上的乘客或工作人員暈船,更有甚者,如果船舶的垂向運(yùn)動(縱搖和垂蕩)達(dá)到某些條件還會對船的安全性構(gòu)成極大的威脅。因此人們研究出了一種適合高速船使用的控制方法——綜合姿態(tài)控制系統(tǒng),可有效地減少高速船的垂向運(yùn)動[2]。綜合姿態(tài)控制系統(tǒng)使用的控制水翼主要有T形水翼和艉壓浪板,艉壓浪板可以控制縱傾角和減少波浪的誘導(dǎo)運(yùn)動,從而控制船舶的垂蕩。
本文主要研究在頂浪情況下的船舶垂向運(yùn)動狀況
安裝在船艏附近T型水翼和船艉的艉壓浪板是產(chǎn)生控制作用的主要裝置,在已有的理論研究和船模實驗的基礎(chǔ)上,利用MATLAB應(yīng)用軟件搭建SIMULINK仿真模塊,對高速船垂向運(yùn)動進(jìn)行仿真并利用遺傳算法對T型水翼和艉壓浪板控制器的部分參數(shù)優(yōu)化選取,實現(xiàn)船舶垂向運(yùn)動的最優(yōu)控制。
2 研究對象與數(shù)學(xué)模型
2.1 研究對象
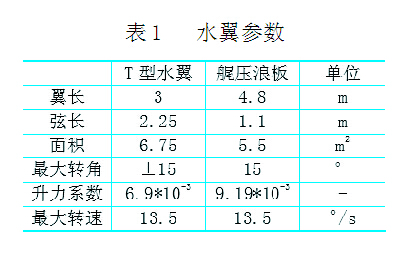
本文根據(jù)一艘高速渡船的數(shù)據(jù)進(jìn)行研究,此船為深V型鋁制單體船,船長110m,船寬14.696m,吃水2.405m,總載重量475t,能一次性運(yùn)送1250名乘客,其速度非常高,大約是40kn或更高,高船速所產(chǎn)生的縱搖與垂蕩運(yùn)動主要依靠安裝在船艏附近的T型水翼和船艉的艉壓浪板來控制。T形水翼有兩個翼面,呈梯形,兩個翼面是對稱的,給出單個翼面的參數(shù)如表1所示。艉壓浪板呈矩形,其參數(shù)如表1所示。
控制水翼T型水翼或艉壓浪板的產(chǎn)生的升力模型如下:
(1)
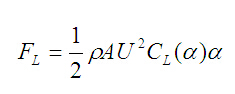

2.2 船舶運(yùn)動數(shù)學(xué)模型
傳統(tǒng)的高速船數(shù)學(xué)模型通常包含垂蕩、縱搖和橫搖的三自由度數(shù)學(xué)模型,由于本文主要研究在頂浪情況下,安裝T型水翼和艉壓浪板后的船舶垂向運(yùn)動狀況,因此針對船舶的縱搖及垂蕩運(yùn)動數(shù)學(xué)模型進(jìn)行研究[3]。
以船體的重心作為附體坐標(biāo)系的原點。 將船體視作剛體,考慮船舶縱傾和波浪對高速船運(yùn)動的影響,在Z 軸方向上利用牛頓第二定律,并以Y 軸為轉(zhuǎn)軸,利用剛體定軸轉(zhuǎn)動定理,可分別得到垂蕩和縱搖運(yùn)動的數(shù)學(xué)模型:

3 仿真
3.1 仿真模型
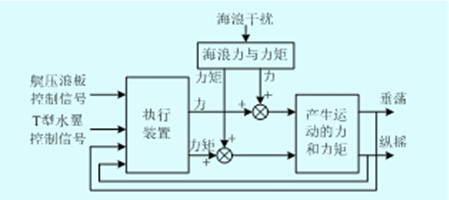
圖1 船舶垂向運(yùn)動仿真模型方框圖
船舶垂向運(yùn)動仿真模型主要分為三部分。一部分用來計算海浪產(chǎn)生的力和力矩,一部分用來計算執(zhí)行裝置產(chǎn)生的力和力矩,一部分用來計算力和力矩產(chǎn)生的垂蕩和縱搖。這樣做的一個好處是執(zhí)行裝置產(chǎn)生的力和力矩容易與船的模型相結(jié)合。整個船舶垂向運(yùn)動仿真模型是一個多變量系統(tǒng),有兩個控制變量,分別為艉壓浪板和T形水翼的控制信號。海浪是外界擾動。船和
執(zhí)行裝置構(gòu)成的系統(tǒng)仿真模型如圖1所示。執(zhí)行裝置需要抵消波浪產(chǎn)生的力和力矩,垂蕩和縱搖信號被反饋給執(zhí)行裝置,執(zhí)行裝置由液壓系統(tǒng)驅(qū)動,需要限定其速度。
3.2 船舶垂向運(yùn)動仿真
船舶垂向運(yùn)動仿真數(shù)學(xué)模型是在公式(2)和(3)的基礎(chǔ)上發(fā)展出來的。兩式聯(lián)立后可得如(4)式所示方程。
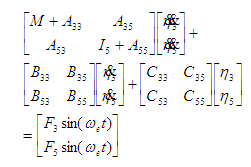
為便于實現(xiàn)時域控制方案的設(shè)計,使用狀態(tài)方程描述該模型,(4)式經(jīng)過推導(dǎo)可取得如式(5)所示的系統(tǒng)狀態(tài)方程
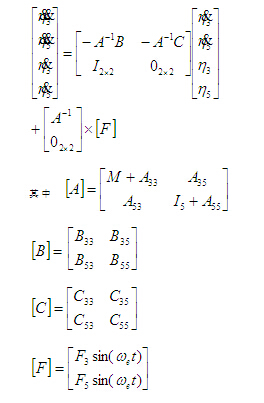
依據(jù)以上數(shù)學(xué)模型,不考慮在一定的壓力和流速下空泡現(xiàn)象的影響,利用MATLAB/SIMULINK開發(fā)了船舶垂向運(yùn)動仿真模型。在40kn航速及4級海況的情況下,研究未安裝控制水翼的船舶縱搖和垂蕩運(yùn)動以及安裝控制水翼且使用固定水翼角的船舶縱搖和垂蕩運(yùn)動并對兩組仿真曲線進(jìn)行對比。
由圖2(a)、(b)可看出安裝控制水翼的船舶垂蕩位移與縱搖角較未安裝的大概減小了30%左右,證明安裝控
制水翼具有減小垂向運(yùn)動的效果,但效果不是很明顯,因此要為控制水翼設(shè)計控制器,以達(dá)到更好的減小垂向運(yùn)動的效果。
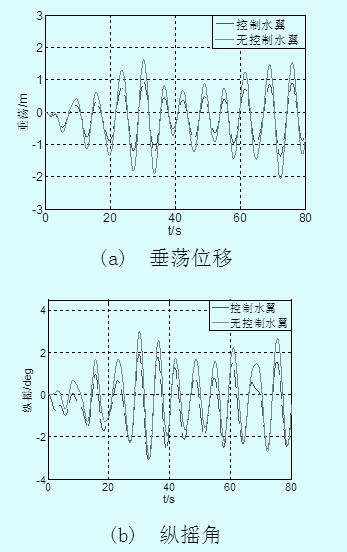
圖2 垂向運(yùn)動曲線
4 控制方案設(shè)計
研究控制方案過程中,將減小船舶垂蕩、縱搖運(yùn)動作為我們的控制目標(biāo)。由于傳統(tǒng)的比例-積分-微分控制(PID)的傳感器會產(chǎn)生許多噪聲,這些噪聲會被微分環(huán)節(jié)放大,所以選擇了PD控制器。采用閉環(huán)控制,將船舶最大垂向加速度或者縱搖和垂蕩運(yùn)動作為控制器輸入。本文研究后一種情況。

圖3 多輸入多輸出控制器方框圖
圖3為多輸入多輸出控制器方框圖。由于需要測量垂蕩和縱搖兩個輸入量,因此采用多輸入多輸出(MIMO控制方法,使用多變量PD控制器實現(xiàn)對艉壓浪板和T型水翼動作的控制以達(dá)到減小船舶垂蕩和縱搖的控制目標(biāo)。以水平面為基準(zhǔn),為艉壓浪板規(guī)定了一個-7.5°的初始位置,當(dāng)有控制信號時,經(jīng)過一個±7.5°范圍內(nèi)的限位信號,艉壓浪板在0°至-15°范圍內(nèi)轉(zhuǎn)動,否則艉壓浪板調(diào)整至以水平面為基準(zhǔn)的-7.5°。當(dāng)有控制信號時T型水翼在±15°范圍內(nèi)運(yùn)動,否則T型水翼調(diào)整至以水平面為基準(zhǔn)的0°
船與執(zhí)行裝置模塊的內(nèi)部結(jié)構(gòu)如圖1 所示。
為便于控制,采用兩個PD控制器,其傳遞函數(shù)和如下:
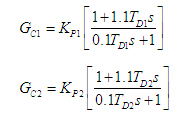
式中分別表示:控制器的增益,控制器的時間常數(shù),控制器的增益,控制器的時間常數(shù)。
遺傳算法對解決復(fù)雜系統(tǒng)優(yōu)化問題,特別是對一些組合優(yōu)化問題的求解有著良好能力[8]。文中控制器參數(shù)的優(yōu)化就是利用遺傳算法求解最優(yōu)化問題解決的。遺傳算法基本流程圖如下所示:

圖4 遺傳算法基本流程圖
由以上流程圖可知,在遺傳算法中,首先通過隨機(jī)方式產(chǎn)生若干個所求問題的數(shù)字編碼來形成初始群體,以此為進(jìn)化起點的第一代群體,并計算每個編碼的個體適應(yīng)度值來對每個個體進(jìn)行數(shù)值評價。這里的適應(yīng)度
值體現(xiàn)并反映了目標(biāo)函數(shù)的尋優(yōu)信息。接下來,從群體中隨機(jī)挑選若干個體作為繁殖過程的樣本集合,選擇機(jī)制應(yīng)保證適應(yīng)度較高的個體保留較多的樣本,而適應(yīng)度較低的個體則保留較少的樣本或被淘汰。在繁殖過程中,利用交叉和變異兩種算子,以一定的交叉概率和變異概率對挑選后的樣本進(jìn)行變換,從而給出新的個體。最后通過新老個體替換產(chǎn)生下一代群體。算法不斷重復(fù)上述評價、選擇、繁殖和替換過程,直到結(jié)束條件得到滿足為止。通常進(jìn)化過程的最后一代群體中適應(yīng)度較高的個體,就是利用遺傳算法求解最優(yōu)化問題的最終結(jié)果。本文就是依據(jù)此算法不斷重復(fù)評價、選擇、繁殖和替換的過程,對控制器參數(shù)進(jìn)行優(yōu)化。
根據(jù)圖3所示的框圖,利用MATLAB開發(fā)仿真環(huán)境,仿真曲線如下圖所示
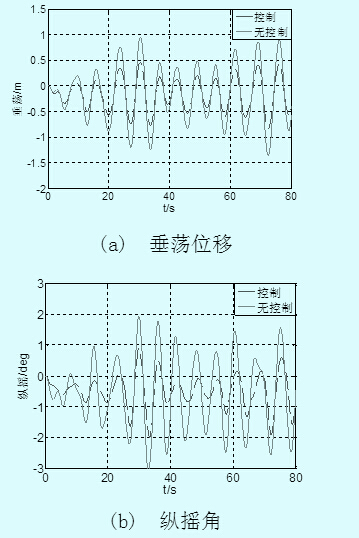
由圖5(a)、(b)可看出加入PD控制后的船舶垂蕩位移與縱搖角較未加入的大概減小了50%左右,證明加入PD控制置具有減小垂向運(yùn)動的效果,從而驗證了控制器的設(shè)計是合理的,能夠減小垂蕩和縱搖。