1 引言
油田配電網中大量使用變頻、整流和開關電源技術制造的節能設備,特別是變頻調速電機、永磁同步電機、變頻器、高頻開關電源等新型節能設備以及非線性電子設備如節能燈、計算機和家用電器等非線性負荷,這些設備在節約能源和提高生產效率的同時,也產生了大量的電力諧波并注入到電網中,使供電質量變壞,對電氣設備產生極大的危害[1]。
針對諧波的危害,可按照配電網的結構、參數和負荷情況,通過電能質量分析,檢測系統的諧波參數和諧波幅值,并通過計算分析判斷電力系統中的電壓電流波形畸變是否控制在允許的范圍內、并給出預警預報。對油田配電網來說,通過頻率掃描,諧波計算可以選擇合適的濾波器,使其對電網的諧波污染控制在標準范圍之內,并預防諧振事故的發生。
隨著我國工業化進程的不斷加快,對電能質量的要求也越來越高,然而現實卻是越來越嚴峻,日趨嚴重的“電力污染”問題不僅對油田配電網的安全穩定的運行造成危害,而且很容易出現某些問題,而造成無法挽回的巨大經濟損失[2]。所以,諧波及其治理將是科研工作者和企業亟待解決的問題。
本文首先針對有天油田配電網的機構特性,建立模擬的諧波產生規律模型,采用神經網絡進行預測預報,
并通過MATALB進行仿真研究。
2 油田配電網諧波系統模型分析
油田配電網結構復雜,網絡系統結構中諧波成分很不相同,畸變波形也是千差萬別,收集所有類型的畸變波形具有很大難度,況且并不是所有的畸變波形都可以用作訓練樣本的。因此很難從建立一個理論上的具有一定精度的數學模型。從對油田配電網中典型的非線性負載所產生的畸變波形的研究分析發現,偶次諧波成分占得比重不大,奇次諧波比重較高且危害很大,并且從分析中發現,任一奇次諧波的幅值一般情況下不會超過基波幅值的50%,諧波次數越高幅值越小。因而在實際測量的時候,我們可以只需要測量其中的奇次諧波。
電力系統中的一些非正弦周期電流可用傅立葉級數展開:
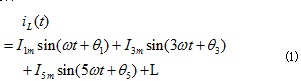
假設奇次諧波以一定的幅度逐漸由0開始遞增,但上限為基波幅度的50%,為簡化模型,油田配電網中5次和7次諧波危害嚴重,因此,本文假設測量諧波電流中的只存在5次諧波,則模型變為:
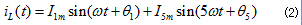
式(2)中,假設初相角一定的情況下,為實現5次諧波幅值的預測,首先確定(2)式中的三個電流變量,等式左邊總的電流值變量和等式右邊的基波電流值變量為輸入,等式右邊的五次諧波電流值變量為輸出,且其幅值可以從基數值按比例增加到50%以上。
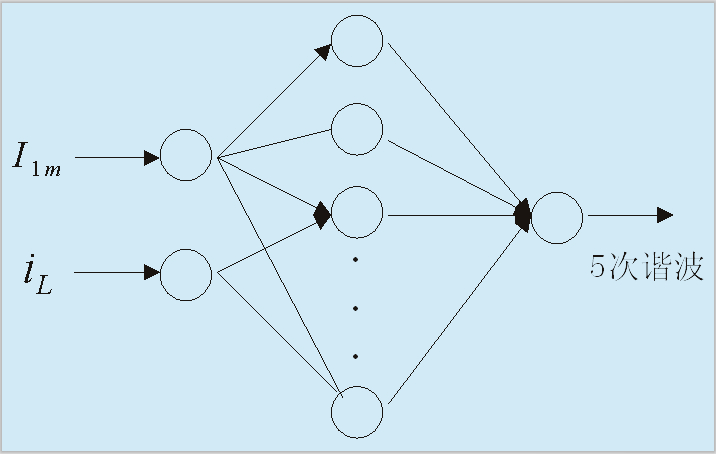
圖1 神經網絡模型結構
神經網絡建模的模型如圖1所示[3],輸入為總的電流值和基波電流值,輸入樣本可以選擇一個周期的隨機值,輸出為5次諧波的幅值。隱含層神經元數量為8個,隱含層個數要根據實際仿真時的訓練樣本數據分析情況進行適當調整,沒有具體的確定方案,以模型輸出誤差和神經網絡權值、閾值作為調整的依據。
3 基于神經網絡的配電網諧波預測研究步驟
根據油田配電網諧波結構的特點,本文采用BP神經網絡進行諧波預測,實現步驟如下[4-5]:
(1) 數據采集與數據的歸一化。
主要包括和油田配電網諧波預測相關的電壓、電流、諧波波次幅值等參數。
(2) 訓練樣本、測試樣本和校驗樣本的建立。
(3) 構建神經網絡,以總電流和基波電流為輸入,以5次諧波幅值為輸出,隱含層選擇8個進行構建神經網絡。
(4) 指定訓練參數進行訓練。
(5) 完成訓練后,就可以調用訓練結果,輸入測試數據,進行測試。
(6) 數據進行反歸一化。
(7) 誤差分析。
4 基于BP神經網絡的諧波發生預測仿真研究
BP網絡作為一種多層前向神經網絡,具有相對比較成熟的理論和算法,是目前在該領域研究比較多的ANN,它可以實現從輸入到輸出的任意非線性映射。這種BP網絡可以在油田配電網系統中用于對諧波進行實時測量。這是因為電網中的被測量是由各次諧波和基波所構成的非正弦周期波形。實現對諧波信息的實時測量,首先需要根據實際的情況選擇相應的網絡結構,然后將待測量的采樣數據施加在經過合理樣本充分訓練后的網絡中。因為相角、幅值變化范圍大并且不具有規律,所以同時改變相角和幅值來對網絡訓練的話,將會增加網絡的負擔,因其同時負擔兩種變化的記憶,如此一來,對諧波測量的速度和精度都會造成很大的影響,因而本文是以假設初相角己經確定為前提的狀態下。
傳統BP網絡收斂速度慢,很難實現大量樣本數據的處理及應用與進行實時預報。因而,與以往常規的梯度下降法不同,本文修正BP網絡的閾值和連接權值采用Levenberg-Marquardt算法(簡稱L-M算法)。L-M算法的基本原理如下: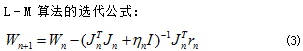
式中:I為單位陣;為一個非負值。依賴于的幅值,該方法光滑地在兩種極端情況之間變法:即Guass-Newton法(當0)和標準梯度法(當)。該式即可作為BP神經網絡的學習訓練方法。
網絡權值和偏差的變化量:
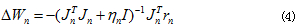
并以此不斷來對網絡進行調整訓練,直至達到目標要求。由式(3)可知,L-M法實際上綜合了Newton法和標準梯度下降法二者的優點,是Newton法和標準梯度下降法的結合。因而,以L-M算法設計的BP網絡在精度及收斂速度方面都有很明顯的優勢。
根據公式(2)模型中的假設,訓練過程中,輸入為總的電流值和基波電流值,根據采樣時間的不同每個周期選擇8對樣本,基波的幅值上限定位1.0,模型的輸出為0.02、0.05和0.5幅值的5次諧波,這樣輸入共24對采樣樣本。
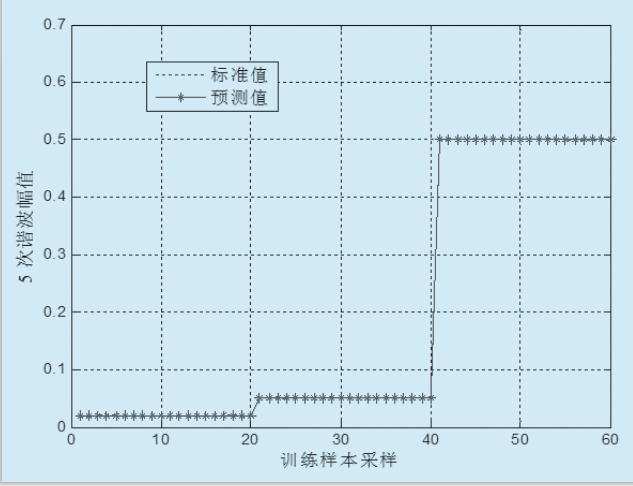
圖2 基于L-M算法的BP神經網絡
諧波預測模型建立
基于L-M算法的網絡模型訓練過程如圖2所示,基于24對訓練樣本的的模型平均誤差為0.0085,達到了一定的精度。為驗證網絡的泛化能力,重新生成40對樣本,輸出諧波幅值分別是0.4和0.08,仿真結果如圖3所示。文中仿真數據采用階躍跟蹤信號,神經網絡模型的仿真結果驗證了L-M算法具有梯度法的全局特性,提供了牛頓法的速度和保證收斂的梯度下降法之間的折衷,收斂的迭代次數少,能快速完成網絡訓練。
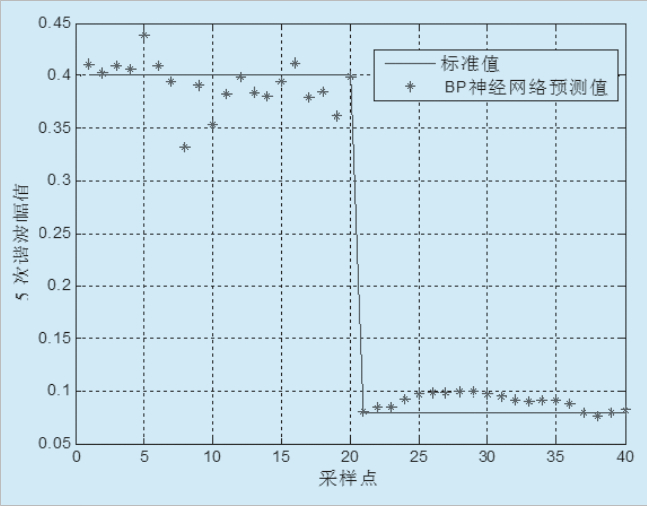
圖3 基于L-M算法的BP神經網絡
諧波預測誤差
5 結束語
本文結合油田的實際需求,建立了油田配電網簡化的數學模型,以五次諧波為研究對象,設為神經網絡的輸出進行仿真研究,采用改進的BP神經網絡方法對油田配電網諧波進行預測預報,并進行了測試樣本驗證。仿真結果驗證了L-M算法的優越性,本文提出的神經網絡預測油田配電網諧波能減少諧波污染,非常具有實用價值。因此,本課題的研究將對于我國在油田節能供電方面技術的提升、供電質量的提高以及高性能供電技術的發展都具有很大的意義,為使電能能夠在油田中得到高效、低污染的應用開辟重要途徑。
參考文獻:
[1] 溫嘉斌,李菁華,宗繼東.小波多分辨率分析在油田配電網諧波檢測中的應用[J].現代電子技術,2008,(3):134-135.2] 戴慶.國內外油田配電系統無功與高次諧波補償理論研究[J].國外油田工程,2002,3(28):48-50.
[3] 于同洋.基于BP神經網絡的營銷風險評估研究[D].武漢理工大學:武漢理工大學,2006.
[4] 許月恒,朱振中.基于BP神經網絡的營銷績效評價研究[J].山東理工大學學報(自然科學版),2008,(2):167-171.
[5] 廉春波.基于相對熵函數準則的BP算法收斂性分析[D].哈爾濱工程大學,2007.