付光杰1,王 依1,任 嬌1,雷 飛2
(1.東北石油大學電氣信息工程學院,黑龍江 大慶 163318;
2.北京工業大學電子信息與控制工程學院,北京 100124)
摘 要:本文以泳池智能救生系統為背景,研究基于小波的泳池水下圖像去噪算法。首先對閾值的選取進行討論,然后分析了閾值函數的選擇對去噪效果的影響,并提出采用改進的非線性閾值函數。最后通過仿真實驗驗證算法的有效性,仿真結果表明,基于非線性閾值函數的小波去噪算法能夠獲得較高的PSNR值,實時性滿足救生需求,能夠較好地應用于泳池水下圖像的處理。
關鍵字:泳池;水下圖像;小波;非線性閾值函數
中圖分類號:TP277 文獻標識碼:A 文章編號:1003-7241(2012)06-0065-04
1 引言
泳池智能救生系統基于水下視覺,對視頻范圍中的目標類型及行為進行分類判斷,以識別出具有溺水特征的目標,從而觸發預警。由于水下圖像信噪比極低,嚴重影響到后期目標提取及特征分析的準確率,使得系統的誤報率較高。基于以上原因,本文以水下圖像為對象,在對其特征進行分析的基礎上,設計了基于小波的圖像去噪算法,為進一步的處理工作奠定基礎。
水下圖像處理技術在近年來得到很大發展。Bazeille等人提出了一種包含同態濾波、小波去噪及各向異性濾波邊緣檢測等一系列過程的自動算法;Chambah等人提出基于自動彩色均衡模型(ACE)的色彩校正方法;Iqbal等人提出了一種基于顏色整合模型的水下圖像增強方法,采用伸展的RGB算法,并將HSI的延伸飽和度和強度應用于增加實際顏色以及解決照明問題;Arnold Bos等人研究了水下圖像中噪聲可能出現的全部范圍,采用同態濾波法處理較黑暗區域的圖像,并取得了較好的效果[1]。
本文以泳池水下圖像為特定場景,采用小波去噪算法對圖像進行處理。小波分析算法在時域和頻域同時具有良好的局部化特性,具有多尺度分析的特點[2],在不同頻率下可以突出圖像的局部特征,從而可以較為有效的去除圖像噪聲并保存邊緣細節的信息完整性,使其較好地適用于水下圖像的去噪。
本文后續部分首先介紹了水下圖像的特征,其次對基于小波的去噪算法進行設計與描述,最后通過仿真實驗對算法的適用性及性能進行分析與討論。
2 水下圖像特征分析
由于水體本身對光線的吸收和散射作用,以及水體中有溶解性有機物和可見的漂浮微粒物的存在,使得水下圖像容易出現照度不均勻、對比度低、噪聲明顯等許多問題,從而造成圖像質量下降。與其他公開水域相比,由于泳池池水晃動,氣泡,水中微粒以及水下倒影的影響,使得泳池水下圖像中光斑、氣泡、懸浮物等干擾更加明顯,信噪比相對較低,但噪聲仍然以高斯白噪聲為主。
3 小波去噪算法
小波去噪方法大體可以分為小波系數萎縮法、投影法和相關法,其中小波系數萎縮法[3]是目前研究最為廣泛的方法,該方法主要是針對于高斯噪聲設計,適合水下圖像噪聲的特征,因而本文采取該方法。圖像經過小波變換后,幅值較大的小波系數反映了圖像的原始信息,幅值較小的小波系數在很大程度上代表的是噪聲,小波去噪算法需要通過設定一個合適的閾值,將小于閾值的小波系數當作噪聲去除,保留絕對值大于閾值的小波系數,然后經過閾值函數映射得到估計系數,對估計系數進行逆變換以實現圖像重構。
3.1 閾值的選取


3.2 閾值函數的選取
在閾值消噪中,閾值函數體現了對小波分解系數的不同處理策略和不同的估計方法,常用的閾值函數有硬閾值和軟閾值函數。
1. 硬閾值函數(Hard threshold)[5]
當小波系數的絕對值小于給定閾值時,令其為0,而大于閾值時,保持其不變,即:

3. 改進的非線性閾值函數(Nonlinear threshold)
硬閾值函數雖然有較好的去噪效果,可是其閾值函數是不連續的,在含有豐富邊緣的圖像中會產生許多人為的噪聲,出現失真現象[6];軟閾值函數雖然克服了硬閾值帶來的不利影響,但造成部分高頻信息丟失,導致圖像邊緣模糊[7]。結合軟硬閾值的不同優缺點,本文采用改進的非線性閾值函數方法[8],其函數表示為:

顯然,通過在0和1之間調節參數e,該閾值函數可以在硬閾值和軟閾值之間進行折衷(如圖1所示),對各種信號均可取得較好的去噪效果。
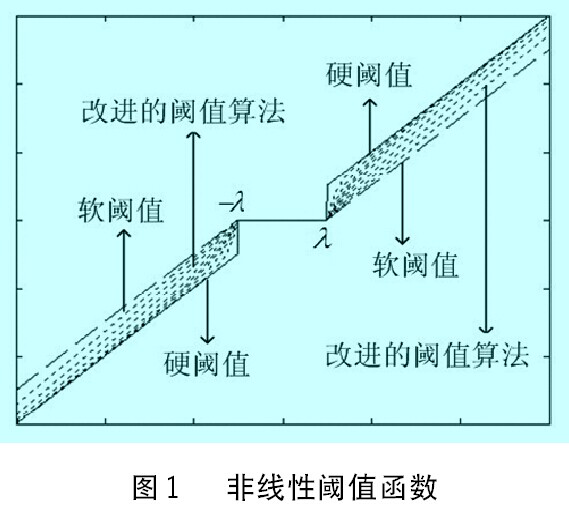
3.3 算法步驟

4 結果及分析
為了驗證小波去噪算法處理泳池水下圖像的有效性,本文以MATLAB為工具進行了實驗分析,目標圖片大小為均352x288像素。實驗中采用sym6小波[9],該小波具有內積計算快速,基函數疊加快速以及良好的空間局部化和頻率局部化特性,保證了圖像信號展開和重構的低復雜度。小波變換分解為3層,經實驗表明,若分解的層數過多,會導致邊緣細節模糊,出現偽Gibbs和振鈴現象[10]。為了比較算法的有效性,實驗對本文所設計的方法分別與硬閾值以及線性閾值(linear threshold)方法(參考文獻2)進行比較,圖2所示為同一圖像經過三種不同的閾值去噪方法進行去噪后的效果對比,通過對其PSNR值的計算,可以看出,相比較于傳統的去噪算法,線性與非線性閾值去噪算法的去噪效果較好。




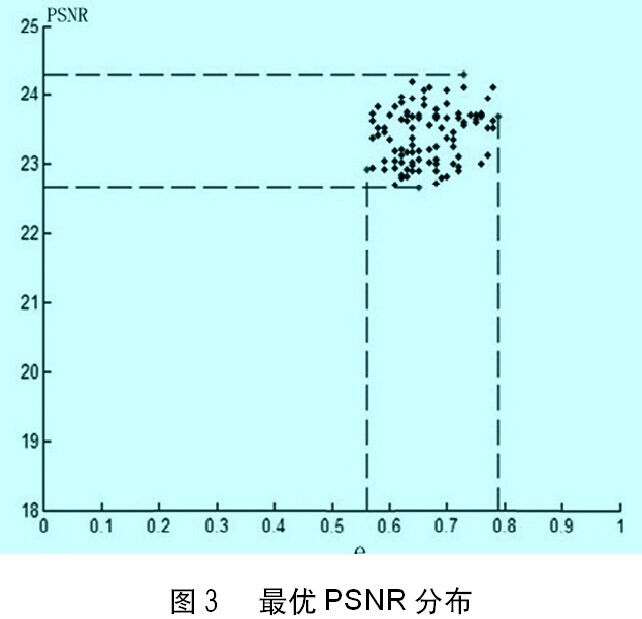
為了進一步探討算法對泳池水下圖像去噪的適應性,本文隨機選取了100幅不同攝像機及場景的圖像,通過調節的值,使得峰值信噪比最大,圖3為值與最高PSNR值的分布情況,由圖可見,對泳池水下圖像,參數e的集中取值范圍為[0.59,0.75],與此對應的PSNR值為[22.82,24.03],去噪效果較好。
三種方法在得到各自最優的PSNR時計算所需時間如表1所示。
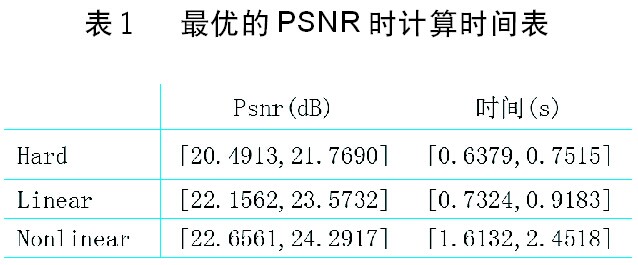
對比可見,改進的非線性閾值去噪法能夠獲得較高的PSNR,但其在計算時間上略劣于硬閾值及線性閾值算法,適用于對實時性要求不高的場合。
5 結束語
由于泳池水下圖像噪聲以高斯噪聲為主,應用小波系數萎縮法能夠獲得良好的去噪效果。算法對閾值函數和參數的選擇較為敏感,閾值函數越精確,去噪效果越明顯,但同時計算復雜度亦增加。對基于泳池救生需要的水下圖像處理而言,在實時性需求允可的范圍內(一般溺水有效救治時間為4-6分鐘),獲得較高質量的圖像,為后期及時準確判斷是否存在異常目標顯得更為重要,從此角度考慮,本文所設計的去噪算法具有一定的實用價值。本文所設計的算法在獲得最佳PSNR值時仍需人工干預,后期的研究工作包括自適應去噪算法的設計,以增加系統的智能性。
參考文獻:
[1] PRABHAKR C.J.PRAVEEN KUMAR P.U.Underwater Image Denoising Using Adaptive Wavelet Subband Thresholding.International Conference on Signal and Image Processing[C].2010,New Delhi,India.322-327.
[2] 高萍,祖靜.基于MATLAB的小波去噪技術淺析[J].科技信息,2007,(6):1-3.
[3] CHEN,G.Y.;BUI,T.D.Multiwavelets denoising using neighboring coefficients[J].Montreal,Canada.2003:211-214.
[4] S.ZHANG,E.SALARI.Image denoising using a neural network based non-filter in wavelet domain[J].Richmond,KY,USA,2005:18-23.
[5] QINWU ZHOU,LIZHUANG LIU,ZHENGZHONG BIAN."Denoise and contrast enhancement of ultrasound speckle image based on wavelet"[J].Journal of Chang'An University,2004,(6):24-26.
[6] JUNMEI ZHONG.Image denoising based on wavelets and multifractals for singularity detection[M].Dct,2005,NY,USA.
[7] XINGMEI LI,GUOPING YAN,and LIANG CHEN."Image denoise based on soft threshold and edge enhancement,"[J].Electronic Measurement Technology.2007,(3):10-12.
[8] 李祥兵,肖合林著.基于MATLAB的小波閾值折衷算法研究[J].電腦開發與應用,2009,(6):4-6.
[9] CHAOYING LIU,HUIBIN WANG and YIXIN WANG."Image denoising based on wavelet edge detection by scale multiplication,"[C].Proceeding of the 2007 IEEE international congerence on integration technology March 2007:20-24.
[10] RAFAEL C.GONZALEZ,and RICHARD E.WOODS."Digital image processing"[M].December,2007.