基于LMI的無人直升機姿態解耦魯棒控制器設計

摘  要:無人直升機是典型的多輸入多輸出系統,具有靜不穩、強耦合、不確定的特點。本文首先基于小擾動理論建立起無人直升機的線性模型;然后運用狀態反饋進行極點配置,實現了對被控對象四通道間的動態解耦;最后設計了基于LMI的無人直升機H∞魯棒姿態控制器,解決了模型參數攝動的問題并進行了仿真驗證。結果表明所設計的姿態控制器性能良好、結構相對簡單,達到ADS-33E-PRF標準LEVEL1的要求。
關鍵詞:無人直升機;極點配置;解耦;線性矩陣不等式(LMI);H∞魯棒控制

中圖分類號:TP302.1    文獻標識碼:A    文章編號:1003-7241(2013)07-0009-05

1  引言 
目前,隨著國民經濟的迅速發展,微型無人直升機在越來越多的領域得到應用,例如在消防、電力線纜巡檢、反恐、救災等場合都已經出現了微型無人直升機的身影[1]。但是微型無人直升機具有不穩定、強耦合、不確定、易進入渦環狀態、操縱功效和抗風能力差的特點,這就導致無人直升機控制難度大,并對飛行控制系統的各種性能均提出嚴峻考驗。另外,隨著進一步的戰事和民用的需求,未來的無人直升機將在極為惡劣的環境下完成復雜的戰術和戰略使命,并且還需要能夠實現精確的自動著陸以及故障狀態下的容錯、自修復控制等,這些都對無人直升機的飛行控制系統提出了極為苛刻的要求。采用傳統基于PID的單回路控制器設計方法顯然已無法滿足高性能無人直升機控制系統的設計要求,因此,進一步加強對無人直升機的先進飛行控制理論和方法的研究,對促進我國無人直升機先進飛行控制技術發展具有重要理論和現實意義。
本論文旨在對面向無人直升機的先進自主飛行控制算法進行研究,為自動飛行控制器的后續設計工作提供指導。基于上述現實原因,本論文的研究內容不僅具有顯著的理論和現實意義而且是一個前沿的研究領域[2]。


2  無人直升機動力學模型 
2.1  操縱力學結構

2.2  動力學模型

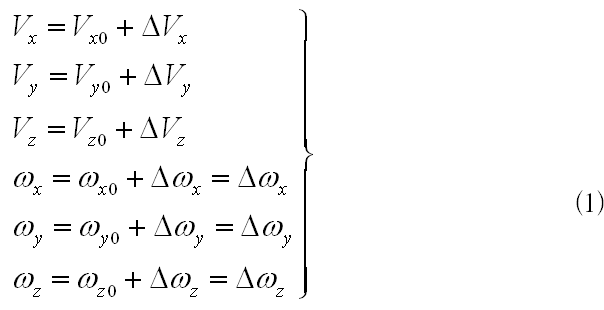
將(1)(2)所描述的參數關系分別帶入到直升機受力分析模型[3]之中,并忽略所有的二階小量,即進行線性化后可以得到下列結果:

綜合式(3)(4)可以得到直升機定常直線飛行時的9階小擾動線化運動方程的標稱狀態空間表達式:

3  基于狀態反饋的極點配置解耦
3.1  狀態反饋解耦控制算法

3.2  期望回路形狀
根據ADS—33E—PRF標準,以LEVEL1為設計目標,可以選擇四個通道上期望回路形狀為[5]:

4  基于LMI的H∞魯棒控制器設計 
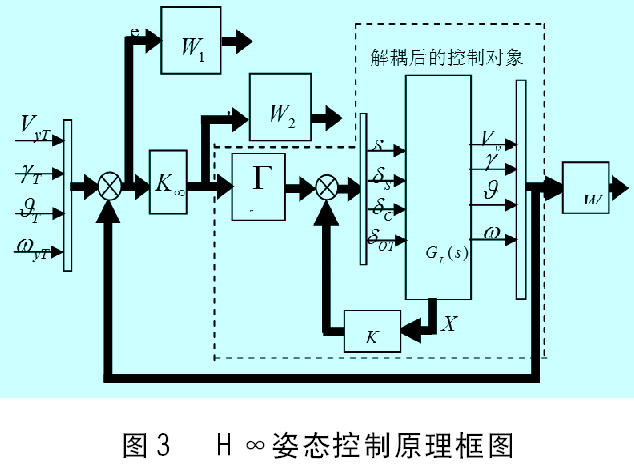
無人直升機具有強烈的靜不穩、強耦合、不確定性特點。采用極點配置方法解決了4通道之間的耦合問題。但是,無人直升機受擾之后模型參數攝動非常明顯,該問題可以采用H∞魯棒控制器給予解決。無人直升機姿態控制器實質上是一個具有良好跟蹤性能的四輸入——四輸出控制器[6,7,8]。原理示意框圖如圖3所示:
其中,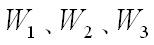為權重函數;為H∞控制器。

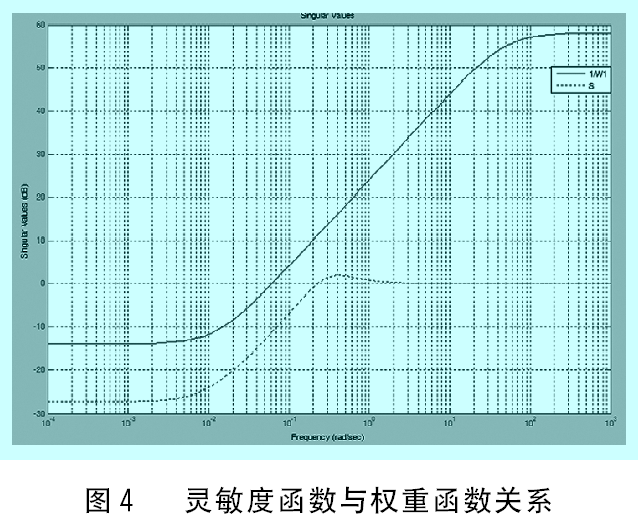
4.1  權重函數選取

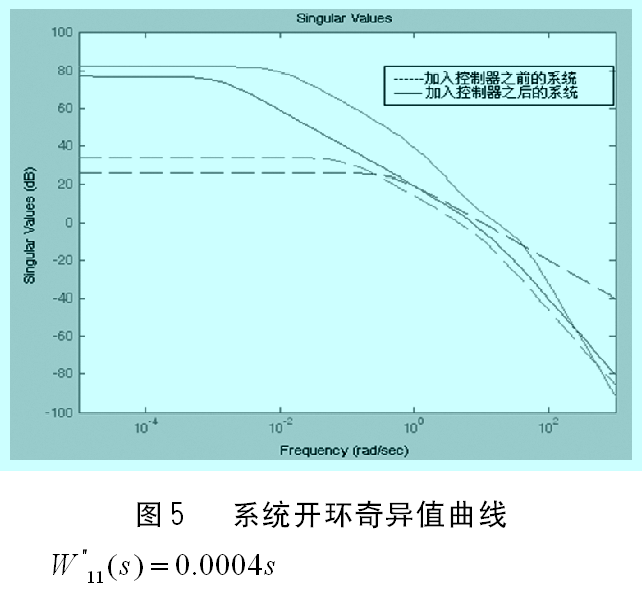
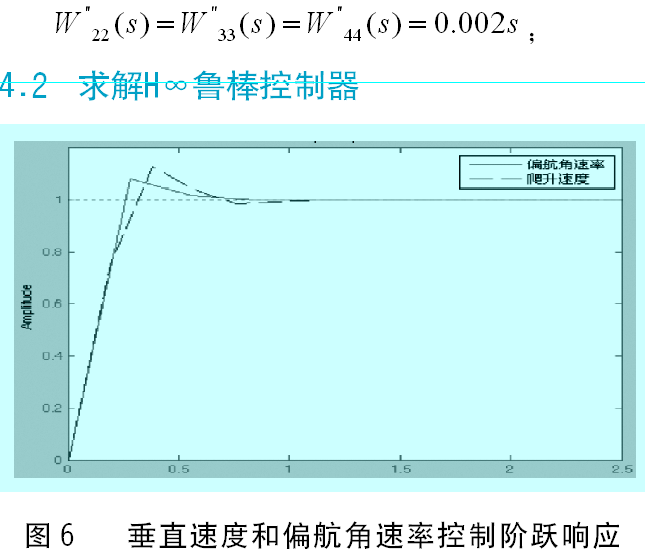
5  仿真實驗結果及性能評估

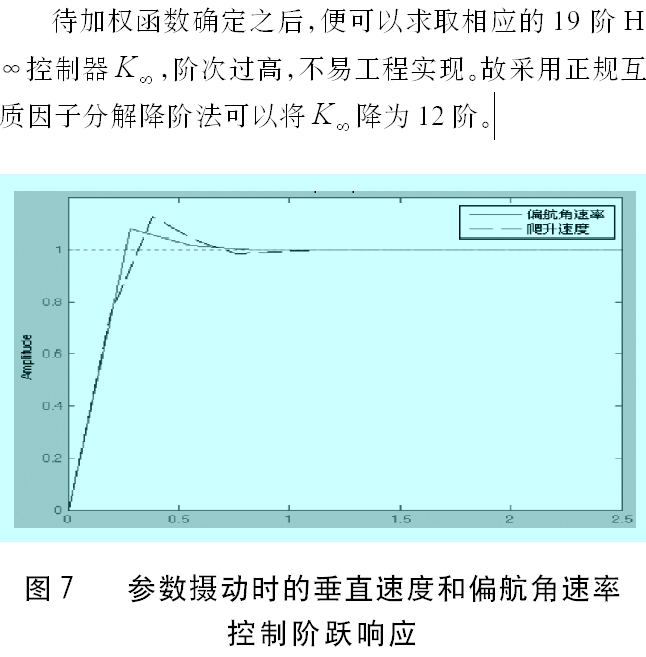
圖7表明動態性能和解耦效果很好,當總距通道和偏航通道存在操縱輸入時,本通道的調節時間很短(0.8s左右)、超調很小(11%左右)并且幾乎不存在通道耦合。圖7表明在被控對象參數攝動時,設計的魯棒控制器仍然可以完成控制任務,效果與攝動之前沒有明顯惡化,并且存在攝動的通道對其它通道的影響不大。


6  結束語
本文首先比較詳細地介紹了小型無人直升機完備的空氣動力學模型建立過程;然后運用狀態反饋進行極點配置,把無人直升機解耦成四個相互獨立的通道;最后運用回路成形理論設計了H∞魯棒控制器,解決了無人直升機模型參數攝動范圍大的問題。論文還對所設計的控制器進行了仿真驗證,結果表明控制效果達到了ADS—33E—PRF標準LEVEL1的要求。本文為設計基于先進算法的無人直升機自動駕駛儀進行了理論方面的探討,為控制器后續工程實現、半實物仿真和試飛驗證奠定基礎。

參考文獻:
[1] LUI SHA,Using Simplicity to Control Complexity[J].IEEE SOFTWARE July/August,2001:20-28.
[2] ISIDORI A,MARCONI L,SERRANI A.Robust nonlinear motion control of a helicopter[J].IEEE Transactions on Automatic Control,2003,48(3):413—426.
[3] 高正,陳仁良.直升機飛行動力學[M].北京:科學出版社,2003.
[4] 鄭大鐘.線性系統理論[M].北京:清華大學出版社,1998.
[5] SHI XIAO-PING, DUAN Hong-JUN.Nonlinear H∞ Attitude Control of Flapping Wing Micro Aerial Vehicle[J].ournal of System Simulation,2007,(10):4499-4503.
[6] VAN DER SCHAFT.L2 Gain Analysis of Nonlinear System and Nonlinear State Feedback H∞ control[J].